
La tabella trigonometrica sin cos tan è una serie di tabelle contenenti il valore trigonometrico o sin cos tangente di un angolo.
Questo articolo mostra una tabella dei valori trigonometrici per il seno cos tan da vari angoli speciali da 0º a 360º (o quello che viene comunemente chiamato l'angolo del cerchio di 360 gradi), in modo che tu non debba più preoccuparti di memorizzarli.
Per quanto riguarda la formula dell'identità trigonometrica, puoi leggerla in questo articolo.
Definizione Sin Cos Tan
Prima di entrare nella tabella dei valori trigonometrici, è una buona idea capire prima i termini trigonometria e sin cos tan.
- La trigonometria è una branca della matematica che studia la relazione tra la lunghezza e l'angolo di un triangolo.
- Il seno (seno) è il rapporto della lunghezza in un triangolo tra la parte anteriore dell'angolo e l'ipotenusa, y / z.
- Cos (coseno) è il rapporto della lunghezza in un triangolo tra il lato dell'angolo e l'ipotenusa, x / z.
- Tan (tangente) è il rapporto delle lunghezze in un triangolo tra la parte anteriore dell'angolo e il lato, y / x.

Tutti i confronti trigonometrici tan sin cos sono limitati a validi solo per triangoli rettangoli o triangoli con un angolo di 90 gradi.
Tavolo trigonometrico Quadrante ad angolo speciale I (0-90 gradi)
| Angolo | 0 º | 30 º | 45 º | 60 º | 90 º |
| Peccato | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Tan | 0 | 1/2 √3 | 1 | √3 | ∞ |
Tavolo trigonometrico con quadrante ad angolo speciale II (90-180 gradi)
| Angolo | 90 º | 120 º | 135 º | 150 º | 180 º |
| Peccato | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Cos | 0 | - 1/2 | - 1/2 √2 | - 1/2 √3 | -1 |
| Tan | ∞ | -√3 | -1 | - 1/3 √3 | 0 |
Tavolo Sin Cos Tan Angolo speciale quadrante III (180-270 gradi)
| Angolo | 180 º | 210 º | 225 º | 240 º | 270 º |
| Peccato | 0 | - 1/2 | - 1/2 √2 | - 1 / 2√3 | -1 |
| Cos | -1 | - 1 / 2√3 | - 1 / 2√2 | - 1/2 | 0 |
| Tan | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Cos Sin Tan Table Special Angle Quadrant IV (270-360 gradi)
| Angolo | 270 º | 300 º | 315 º | 330 º | 360 º |
| Peccato | -1 | -½√3 | -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 |
| Tan | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
Quindi l'elenco completo delle tabelle trigonometriche da tutti gli angoli speciali da 0 a 360 gradi.
Leggi anche: Processo del meccanismo di visione umana e suggerimenti per la cura degli occhiÈ possibile utilizzare questa tabella per facilitare l'attività nel calcolo o nell'analisi della trigonometria in matematica.
Richiamo della tavola trigonometrica ad angolo speciale senza memorizzazione
In effetti, non devi preoccuparti di memorizzare tutti i valori trigonometrici da ogni angolazione.
Tutto ciò di cui hai bisogno è un concetto di comprensione di base che puoi usare per scoprire il valore trigonometrico di qualsiasi angolo particolare.
Hai solo bisogno di ricordare i componenti della lunghezza del lato del triangolo con angoli speciali 0, 30, 45, 60 e 90 gradi.
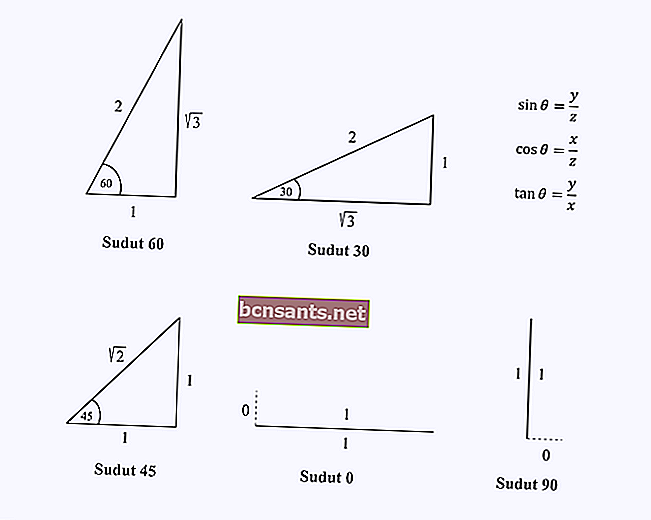
Supponiamo di voler trovare il valore di cos (60).
Devi solo ricordare la lunghezza del lato del triangolo con un angolo di 60 gradi, quindi eseguire l'operazione del coseno, che è x / z su quel triangolo.
Dalla figura, vedrai che il valore di cos 60 = 1/2.
Facile vero?
Per gli angoli negli altri quadranti, il metodo è lo stesso e devi solo regolare il segno positivo o negativo di ogni quadrante.
Tavolo A Forma Di Cerchio
Se la tabella cos sin tan sopra è troppo lunga da ricordare, anche se il metodo del concetto di angolo speciale che ritieni sia ancora difficile ...
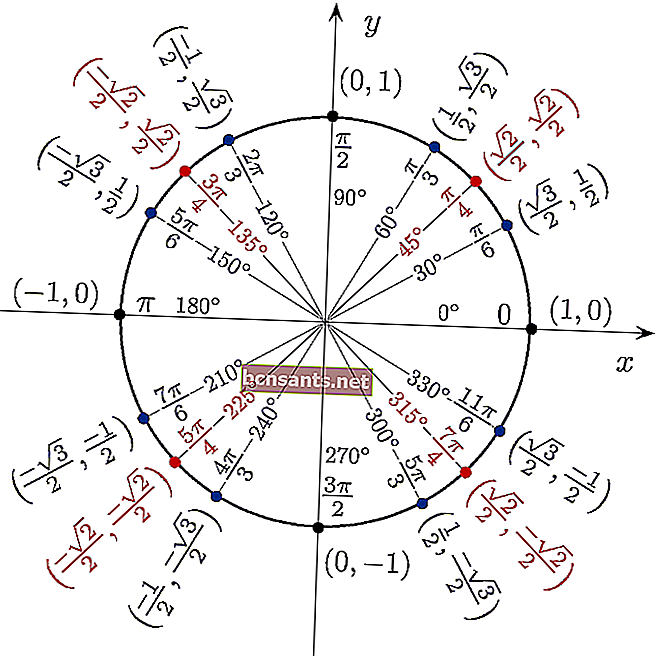
È possibile utilizzare la tabella trigonometrica sotto forma di un cerchio per vedere direttamente il valore di sin cos tan da un angolo di 360 gradi.
Trucchi rapidi per memorizzare tabelle trigonometriche
Oltre ai metodi sopra, c'è ancora un altro metodo che puoi usare per ricordare facilmente le tabelle delle formule trigonometriche.
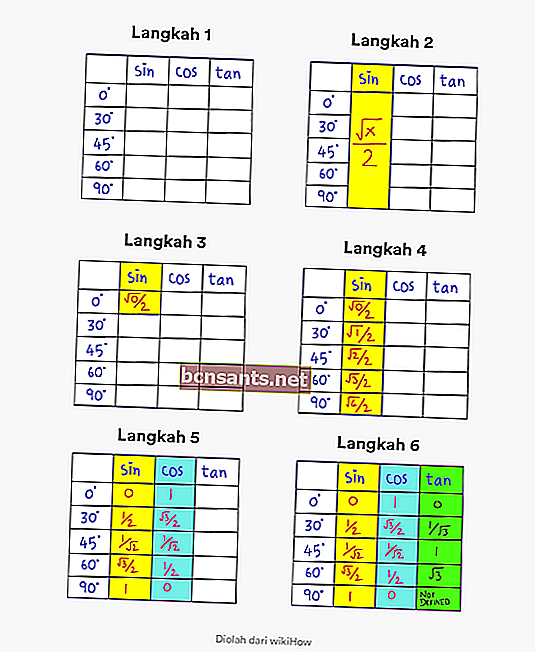
I passaggi da eseguire sono i seguenti:
- Passaggio 1 . Crea una tabella che contenga angoli da 0 a 90 gradi e colonne con la descrizione sin cos tan
- Passaggio 2 . Nota che la formula generale per il peccato con un angolo compreso tra 0 e 90 gradi è √x / 2.
- Passaggio 3 . Cambia il valore x a 0 su √x / 2 nella primissima colonna. Angolo in alto a sinistra.
- Passaggio 4. Compilare in sequenza modificando la x in 0, 1, 2, 3, 4 nella colonna del peccato. Quindi hai il valore trigonometrico completo sin
- Passaggio 5 . Per trovare il valore di cos, tutto ciò che devi fare è invertire l'ordine nella colonna del peccato.
- Passaggio 6 . Per trovare il valore di tan, tutto ciò che devi fare è dividere il valore sin per il valore cos.
Quale è più facile per te da capire per ricordare il valore trigonometrico di tan sin cos?
In ogni caso, scegli quello che è più facile da capire. Perché ogni persona ha uno stile di apprendimento diverso.
Tabelle per tutti gli angoli
Se nelle tabelle sopra i valori mostrati sono solo i valori trigonometrici di angoli speciali, allora questa tabella mostra tutti i valori trigonometrici di tutti gli angoli da 0 a 90 gradi.
| Angolo | Radianti | Peccato | Cos | Tan |
| 0 ° | 0 | 0 | 1 | 0 |
| 1 ° | 0.01746 | 0.01746 | 0.99985 | 0.01746 |
| 2 ° | 0.03492 | 0.03491 | 0.99939 | 0.03494 |
| 3 ° | 0.05238 | 0.05236 | 0.99863 | 0.05243 |
| 4 ° | 0.06984 | 0.06979 | 0.99756 | 0.06996 |
| 5 ° | 0.0873 | 0.08719 | 0.99619 | 0.08752 |
| 6 ° | 0.10476 | 0.10457 | 0.99452 | 0.10515 |
| 7 ° | 0.12222 | 0.12192 | 0.99254 | 0.12283 |
| 8 ° | 0.13968 | 0.13923 | 0.99026 | 0.1406 |
| 9 ° | 0.15714 | 0.1565 | 0.98768 | 0.15845 |
| 10 ° | 0.1746 | 0.17372 | 0.9848 | 0.1764 |
| 11 ° | 0.19206 | 0.19089 | 0.98161 | 0.19446 |
| 12 ° | 0.20952 | 0.20799 | 0.97813 | 0.21265 |
| 13 ° | 0.22698 | 0.22504 | 0.97435 | 0.23096 |
| 14 ° | 0.24444 | 0.24202 | 0.97027 | 0.24943 |
| 15 ° | 0.26191 | 0.25892 | 0.9659 | 0.26806 |
| 16 ° | 0.27937 | 0.27575 | 0.96123 | 0.28687 |
| 17 ° | 0.29683 | 0.29249 | 0.95627 | 0.30586 |
| 18 ° | 0.31429 | 0.30914 | 0.95102 | 0.32506 |
| 19 ° | 0.33175 | 0.32569 | 0.94548 | 0.34448 |
| 20 ° | 0.34921 | 0.34215 | 0.93965 | 0.36413 |
| 21 ° | 0.36667 | 0.35851 | 0.93353 | 0.38403 |
| 22 ° | 0.38413 | 0.37475 | 0.92713 | 0.40421 |
| 23 ° | 0.40159 | 0.39088 | 0.92044 | 0.42467 |
| 24 ° | 0.41905 | 0.40689 | 0.91348 | 0.44543 |
| 25 ° | 0.43651 | 0.42278 | 0.90623 | 0.46652 |
| 26 ° | 0.45397 | 0.43854 | 0.89871 | 0.48796 |
| 27 ° | 0.47143 | 0.45416 | 0.89092 | 0.50976 |
| 28 ° | 0.48889 | 0.46965 | 0.88286 | 0.53196 |
| 29 ° | 0.50635 | 0.48499 | 0.87452 | 0.55458 |
| 30 ° | 0.52381 | 0.50018 | 0.86592 | 0.57763 |
| 31 ° | 0.54127 | 0.51523 | 0.85706 | 0.60116 |
| 32 ° | 0.55873 | 0.53011 | 0.84793 | 0.62518 |
| 33 ° | 0.57619 | 0.54483 | 0.83854 | 0.64974 |
| 34 ° | 0.59365 | 0.55939 | 0.8289 | 0.67486 |
| 35 ° | 0.61111 | 0.57378 | 0.81901 | 0.70057 |
| 36 ° | 0.62857 | 0.58799 | 0.80887 | 0.72693 |
| 37 ° | 0.64603 | 0.60202 | 0.79848 | 0.75396 |
| 38 ° | 0.66349 | 0.61587 | 0.78785 | 0.78172 |
| 39 ° | 0.68095 | 0.62953 | 0.77697 | 0.81024 |
| 40 ° | 0.69841 | 0.643 | 0.76586 | 0.83958 |
| 41 ° | 0.71587 | 0.65628 | 0.75452 | 0.86979 |
| 42 ° | 0.73333 | 0.66935 | 0.74295 | 0.90094 |
| 43 ° | 0.75079 | 0.68222 | 0.73115 | 0.93308 |
| 44 ° | 0.76825 | 0.69488 | 0.71913 | 0.96629 |
| 45 ° | 0.78571 | 0.70733 | 0.70688 | 1.00063 |
| 46 ° | 0.80318 | 0.71956 | 0.69443 | 1.0362 |
| 47 ° | 0.82064 | 0.73158 | 0.68176 | 1.07308 |
| 48 ° | 0.8381 | 0.74337 | 0.66888 | 1.11137 |
| 49 ° | 0.85556 | 0.75494 | 0.6558 | 1.15117 |
| 50 ° | 0.87302 | 0.76627 | 0.64252 | 1.1926 |
| 51 ° | 0.89048 | 0.77737 | 0.62904 | 1.2358 |
| 52 ° | 0.90794 | 0.78824 | 0.61537 | 1.28091 |
| 53 ° | 0.9254 | 0.79886 | 0.60152 | 1.32807 |
| 54 ° | 0.94286 | 0.80924 | 0.58748 | 1.37748 |
| 55 ° | 0.96032 | 0.81937 | 0.57326 | 1.42932 |
| 56 ° | 0.97778 | 0.82926 | 0.55887 | 1.48382 |
| 57 ° | 0.99524 | 0.83889 | 0.5443 | 1.54122 |
| 58 ° | 1.0127 | 0.84826 | 0.52957 | 1.60179 |
| 59 ° | 1.03016 | 0.85738 | 0.51468 | 1.66584 |
| 60 ° | 1.04762 | 0.86624 | 0.49964 | 1.73374 |
| 61 ° | 1.06508 | 0.87483 | 0.48444 | 1.80587 |
| 62 ° | 1.08254 | 0.88315 | 0.46909 | 1.8827 |
| 63 ° | 1.1 | 0.89121 | 0.4536 | 1.96476 |
| 64 ° | 1.11746 | 0.89899 | 0.43797 | 2.05265 |
| 65 ° | 1.13492 | 0.9065 | 0.4222 | 2.14707 |
| 66 ° | 1.15238 | 0.91373 | 0.40631 | 2.24884 |
| 67 ° | 1.16984 | 0.92069 | 0.3903 | 2.35894 |
| 68 ° | 1.1873 | 0.92736 | 0.37416 | 2.4785 |
| 69 ° | 1.20476 | 0.93375 | 0.35792 | 2.60887 |
| 70 ° | 1.22222 | 0.93986 | 0.34156 | 2.75169 |
| 71 ° | 1.23968 | 0.94568 | 0.3251 | 2.90892 |
| 72 ° | 1.25714 | 0.95121 | 0.30854 | 3.08299 |
| 73 ° | 1.2746 | 0.95646 | 0.29188 | 3.27686 |
| 74 ° | 1.29206 | 0.96141 | 0.27514 | 3.49427 |
| 75 ° | 1.30952 | 0.96606 | 0.25831 | 3.73993 |
| 76 ° | 1.32698 | 0.97043 | 0.2414 | 4.01992 |
| 77 ° | 1.34444 | 0.97449 | 0.22442 | 4.34219 |
| 78 ° | 1.36191 | 0.97826 | 0.20738 | 4,71734 |
| 79 ° | 1.37937 | 0.98173 | 0.19026 | 5.15984 |
| 80 ° | 1.39683 | 0.98491 | 0.1731 | 5.68998 |
| 81 ° | 1.41429 | 0.98778 | 0.15587 | 6.33709 |
| 82 ° | 1.43175 | 0.99035 | 0.1386 | 7.14523 |
| 83 ° | 1.44921 | 0.99262 | 0.12129 | 8.18379 |
| 84 ° | 1.46667 | 0.99458 | 0.10394 | 9.56868 |
| 85 ° | 1.48413 | 0.99625 | 0.08656 | 11.5092 |
| 86 ° | 1.50159 | 0.99761 | 0.06915 | 14,4259 |
| 87 ° | 1.51905 | 0.99866 | 0.05173 | 19.3069 |
| 88 ° | 1.53651 | 0.99941 | 0.03428 | 29.153 |
| 89 ° | 1.55397 | 0.99986 | 0.01683 | 59.4189 |
| 90 ° | 1.57143 | 1 | 0 | ∞ |
Spero che questa spiegazione trigonometrica possa esserti utile.
Questo materiale sarà di grande utilità per varie applicazioni in matematica e fisica avanzate.
Puoi anche imparare altri materiali scolastici a Saintif, come numeri primi, conversioni di unità, formule rettangolari e così via.
Riferimento
- Trigonometria - Wikipedia
- Strumenti matematici - Trigonometria
