Raccolta di formule matematiche per la classe 6 SD

La seguente raccolta di formule matematiche per il grado 6 SD è composta da:

• Una raccolta di formule di volume per la costruzione dello spazio, formula per la scala
• Calcolo dell'area piana
• Operazioni con numeri interi
• Formule per operazioni di conteggio di numeri misti
• La formula per FPB e KPK è due numeri
• Elaborazione e presentazione dei dati
• Formule di sistema di coordinate, volume e tempo
• Somma e sottrazione di frazioni e determinazione della radice quadrata di numeri cubici.

Formule matematiche di grado 6 Calcola il volume della costruzione di una stanza

Nome Build Space	Formule di volume
Tubo	V = phi r² xt
Prima triangolo verticale	V = Area della base x Altezza

Scala di calcolo della raccolta di formule matematiche di classe 6

Formule di scala	= Distanza sull'immagine (mappa) / Distanza effettiva
Formule di distanza in Fig	= Distanza effettiva x Scala
Formule di distanza effettiva	= Distanza sull'immagine (mappa) / Scala

Raccolta di formule per calcolare l'area di un appartamento

Figura bidimensionale	Formula dell'area
Costruisci un quadrato piatto	L = lato x lato = s²
Costruisci un triangolo piatto	L = ½ base x altezza
Costruisci un cerchio piatto	L = phi x r²
Costruzione trapezoidale	L = ½ t × (a + b)
Build Flat Kite - Kite	L = ½ xd 1 xd 2
Costruisci parallelogramma piatto	L = Base x Altezza
Alzati rombo piatto	L = ½ xd 1 xd 2
Costruisci rettangolo piatto	L = Lunghezza x Larghezza

Raccolta di formule di operazioni intere SD di classe 6

• Proprietà commutative dell'addizione, formule generali: a + b = b + a

Ad esempio: 2 + 4 = 4 + 2 = 6 o 5 + 10 = 10 + 5 = 15

• Natura commutativa della moltiplicazione, formule generali: axb = bxa

Ad esempio: 3 x 5 = 5 x 3 = 15 o 10 x 2 = 2 x 10 = 20

• Proprietà distributive dalla moltiplicazione all'addizione

Formula generale: ax (b + c) = (axb) + (axc)

Esempio :

2 x (5 + 10)	= 2 x 5 + 2 x 10
	= 10 + 20
	= 30

• Natura distributiva dalla moltiplicazione alla sottrazione

Formula generale: ax (b - c) = (axb) - (axc)

Esempio :

2 x (10 - 5)	= 2 x 10 - 2 x 5
	= 20 + 10
	= 10

Raccolta di formule per operazioni di calcolo con numeri misti

L'operazione per calcolare numeri misti ha 2 condizioni, vale a dire, tra le altre:

Leggi anche: Caratteristiche dei pianeti nel sistema solare (COMPLETO) con immagini e spiegazioni

Per prima cosa, se ci sono parentesi (), fai prima quello che c'è dentro le parentesi.

Secondo, se non ci sono parentesi (), prima fai moltiplicazione e divisione, quindi addizione e sottrazione.

Esempio:

= 7000 - 40 x 100: 4 + 200		= 1000: 10 x 2 - (200 + 50)
= 7000 - 1000 + 200		= 1000: 10 x 2 - 150
= 6200	O	= 100 x 2-150
		= 200-150
		= 50

La formula per FPB e KPK è due numeri

Come determinare l'FPB (Fattore comune più grande) Due numeri, tra gli altri, Trova il fattore in ciascuno di questi numeri, determina il Fattore comune dei due numeri e Moltiplica il Fattore comune (stesso fattore) che ha la potenza più piccola.

Esempio :

27	= 3³
18	= 2 x 3²

Il fattore comune per l'FPB di due numeri è 3 e la potenza minima è 3² = 9

Come determinare il LCM (minimo comune multiplo) per due numeri, tra gli altri, trova il fattore primo di ciascuno di questi numeri, moltiplica tutti i fattori e fattori uguali, viene scelto il rango più alto.

Ad esempio: valori KPK 12 e 15

12	= 2² x 3
15	= 3 x 5

Valore LCM due numeri sopra: 2² x 3 x 5 = 50

Elaborazione e presentazione dei dati

La modalità è il valore che appare di più.

Il valore minimo è il valore più piccolo e più basso di tutti i dati.

Il valore massimo è il valore più alto di tutti i dati in esso contenuti.

La media è per la media viene ricercata sommando tutti i campioni divisi per il numero di campioni.

• Trovare il sistema di coordinate
• L'asse x è anche chiamato Absis (x) e per l'asse y è anche chiamato Ordinate (y).
• Un piano in coordinate cartesiane sarà formato da 2 assi, ovvero l'asse verticale (asse y) e l'asse orizzontale (asse x).
• Dal punto zero l'asse verticale sarà verso l'alto e l'asse orizzontale sarà a destra che ha un valore positivo.
• Dal punto zero l'asse verticale scenderà e l'asse orizzontale andrà a sinistra che ha un valore negativo.
• La ricerca delle coordinate di un oggetto può essere trovata trovando la posizione sull'asse x a destra oa sinistra con la posizione sull'asse y in alto o in basso.

Leggi anche: Class 6 Mathematics Questions (+ Discussion) SD UASBN - Complete

Relazione tra unità di volume

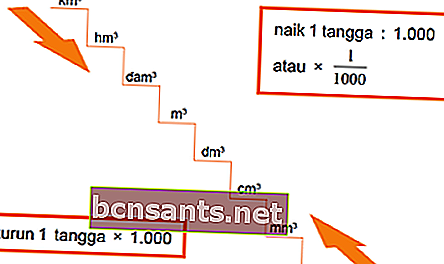
Esempio:

1 km3 = 1.000 hm3 (giù per 1 scala)

1 m3 = 1.000.000 cm3 (giù per 2 scale)

1 m3 = 1 / 1.000 diga3 (su 1 scala)

1 m3 = 1 / 1.000.000 hm3 (su 2 scale)

Volume in litri

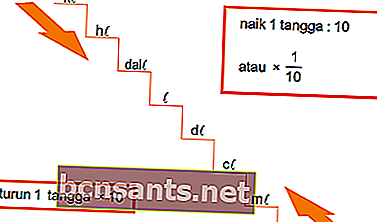
Unità di tempo

Un minuto	= 60 secondi
Un'ora	= 60 minuti
Un giorno	= 24 ore
Una settimana	= 7 giorni
Un mese	= 30 giorni / 31 giorni
Un mese	= 4 settimane
Un anno	= 52 settimane
Un anno	= 12 mesi
One Windu	= 8 anni
Un decennio	= 10 anni
Un decennio	= 10 anni
Un secolo	= 100 anni
Un millennio	= 1000 anni

Conversione di secondi

• 1 minuto = 60 secondi
• 1 ora = 3600
• 1 giorno = 86400
• 1 mese = 2 592000 secondi
• 1 anno = 31104000 secondi

Addizione e sottrazione di frazioni

Per poter aggiungere e sottrarre frazioni, prima equalizza i denominatori.

Esempio:

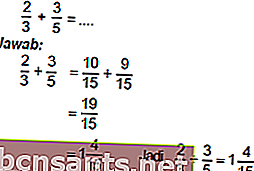
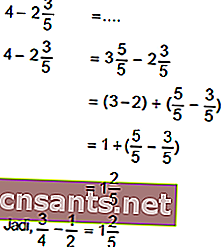
Moltiplicare e dividere le frazioni

Moltiplicare le frazioni è abbastanza facile. Il numeratore moltiplicato per il numeratore. Il denominatore moltiplicato per il denominatore. Se può essere semplificato, semplifica:

La divisione frazionaria equivale a moltiplicare per il divisore della frazione.

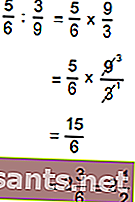
Trova la radice cubica di un numero cubico

13 viene letto come un cubo = 1 × 1 × 1 = 1

23 è letto come due alla potenza di tre = 2 × 2 × 2 = 8

33 viene letto come tre cubi = 3 × 3 × 3 = 27

43 è letto come quattro alla potenza di tre = 4 × 4 × 4 = 64

53 è letto come cinque alla potenza di tre = 5 × 5 × 5 = 125

1, 8, 27, 64, 125 e così via sono numeri cubici o potenze di 3

Addizione e sottrazione

23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)

= 8 + 27

= 35

63-43 = (6 × 6 × 6) - (4 × 4 × 4)

= 216 - 64

= 152

Moltiplicazione e divisione

23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)

= 8 × 64

= 512

63: 23 = (6 × 6 × 6): (2 × 2 × 2)

= 216: 8

= 27

Questa è una raccolta di formule matematiche della scuola elementare di 6 ° grado che spesso appaiono nelle domande dell'Esame Finale Nazionale (UAN) e dell'Esame Nazionale (UN). Può essere utile.