
La formula per il triangolo per trovare l'area della forma è 1/2 x base x altezza, per trovare il perimetro del triangolo puoi trovare la lunghezza di ciascun lato del triangolo.
In Matematica, ci vengono insegnate varie forme. Uno di questi è una forma triangolare. La forma del triangolo è la forma più semplice tra i vari tipi di forme.
Un triangolo è formato da tre lati con tre angoli delimitati da un segmento. Inoltre, l'angolo totale del triangolo è di 180 gradi.
Esistono diversi tipi di triangoli. In base alla lunghezza dei lati, ci sono triangoli equilateri con lunghezze laterali uguali, triangoli isosceli con due lati uguali delle gambe e qualsiasi triangolo con lunghezze diverse di tre lati.
Nel frattempo, in base all'angolo, c'è un triangolo acuto con un angolo inferiore a 90 gradi, un triangolo ottuso con un angolo superiore a 90 gradi e un triangolo rettangolo con un angolo di 90 gradi.
Per quanto riguarda i triangoli, ci sono diversi componenti che devono essere conosciuti tra cui l'area e il perimetro del triangolo. Quanto segue è una spiegazione dell'area e del perimetro del triangolo insieme a un esempio del problema.
Area del triangolo

Area, area o area è una quantità che esprime la dimensione bidimensionale, ovvero una parte della superficie chiaramente definita da una curva o linea chiusa.
L'area del triangolo è la dimensione del triangolo stesso. La seguente è la formula per l'area di un triangolo:
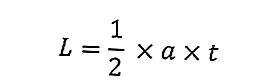
dove L è l'area del triangolo (cm 2 ), a è la base del triangolo (cm) e h è l'altezza del triangolo (cm).
Esempio di problema dell'area di un triangolo
Problema di esempio 1
C'è un triangolo acuto la cui lunghezza di base è a = 10 cm e ha anche un'altezza di h = 8 cm. Calcola l'area del triangolo.
Leggi anche: Animali: caratteristiche, tipi, esempi [spiegazione COMPLETA]Soluzione:
Se: a = 10 cm, h = 8 cm
Ricercato: l'area del triangolo?
Risposta:
L = ½ xaxt
= ½ x 10 x 8
= 40 cm2
Quindi, l'area del triangolo acuto è di 40 cm2
Problema di esempio 2
Un triangolo rettangolo ha una base di 15 cm e un'altezza di 20 cm. Trova e calcola l'area del triangolo rettangolo.
Soluzione:
Se: a = 15 cm, h = 20 cm
Ricercato: l'area del triangolo?
Risposta:
L = ½ xaxt
= ½ x 15 x 20
= 150 cm2
Quindi, l'area del triangolo rettangolo è 150 cm2
Problema di esempio 3
Un triangolo ottuso con una base di 8 cm e un'altezza di 3 cm, qual è quindi l'area del triangolo?
Soluzione:
Sai: a = 8 cm, h = 3 cm
Ricercato: l'area del triangolo?
Risposta:
L = ½ xaxt
= ½ x 8 x 3
= 12 cm2
Quindi, l'area del triangolo ottuso è di 12 cm2
Problema di esempio 4
Un triangolo isoscele con la stessa lunghezza del lato è di 13 cm e la base del triangolo è di 10 cm. Qual è l'area del triangolo isoscele?
Soluzione:
Sai: s = 13 cm, a = 10 cm
Ricercato: l'area del triangolo?
Risposta:
L'altezza del triangolo non è nota, quindi usiamo la formula pitagorica per trovare l'altezza del triangolo:

Poiché l'altezza del triangolo è nota, allora:
L = ½ xaxt
= ½ x 10 x 12
= 60 cm2
Quindi, l'area del triangolo isoscele è di 60 cm2
Perimetro del triangolo

Il perimetro è il numero di lati in una forma bidimensionale. Quindi, il perimetro del triangolo è la somma dei lati del triangolo stesso.
Ecco la formula per il perimetro di un triangolo:
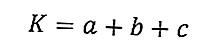
dove K è il perimetro del triangolo (cm) e a, b, c sono le lunghezze dei lati del triangolo (cm).
Esempio di perimetro di un triangolo
Problema di esempio 1
Un triangolo equilatero ha lati lunghi 15 cm. Qual è il perimetro del triangolo?
Soluzione:
Sai: lunghezza laterale = 15 cm
Alla domanda: circonferenza =….?
Risposta:
K = lato a + lato b + lato c
poiché è un triangolo equilatero, le lunghezze dei tre lati sono uguali.
K = 15 + 15 + 15
= 45 cm
Quindi , il perimetro del triangolo equilatero è di 45 cm
Leggi anche: L'interazione sociale è: definizione e spiegazione completeProblema di esempio 2
Un triangolo arbitrario ha lati di 3 cm, 5 cm e 8 cm. Calcola il perimetro del triangolo.
Soluzione:
Sai: a = 3 cm, b = 5 cm e c = 8 cm
Alla domanda: circonferenza =….?
Risposta:
K = lato a + lato b + lato c
= 3 + 5 + 8
= 16 cm
Quindi, il perimetro del triangolo è di 16 cm
Problema di esempio 3
Un triangolo isoscele ha lati pari a 10 cm e una base di 6 cm. Calcola il perimetro del triangolo isoscele.
Soluzione:
Sai: i lati sono lunghi 10 cm e lunghi 6 cm
Alla domanda: circonferenza =….?
Risposta:
K = lato a + lato b + lato c
poiché il triangolo è isoscele, allora ci sono due lati della stessa lunghezza, cioè 10 cm, quindi K = 10 + 10 + 6 = 26 cm
Quindi, il perimetro del triangolo isoscele è di 26 cm
Problema di esempio 4
Un triangolo isoscele ha un'altezza di 8 cm e una base di 12 cm. Calcola il perimetro del triangolo.
Soluzione:
Sai: l'altezza del triangolo h = 8 cm
lato della base a = 12 cm
Alla domanda : circonferenza =….?
Risposta:
K = lato a + lato b + lato c
I due lati del triangolo sono sconosciuti, quindi usiamo la formula pitagorica per trovare la lunghezza di quel lato.

K = 10 + 10 + 12
K = 32 cm
Quindi, il perimetro del triangolo isoscele è di 32 cm
Questa è una spiegazione dell'area di un triangolo e del perimetro del triangolo insieme ad esempi e discussioni. Può essere utile.
