
La formula per il perimetro è K = 2 × π × r, dove K = la circonferenza del cerchio, π = la costante pi (3.14) er = il raggio del cerchio. Quella che segue è una spiegazione più completa accompagnata da un problema di esempio.
L'invenzione della ruota è una delle scoperte fondamentali sull'importanza delle forme circolari nella vita di tutti i giorni.
Non solo ruote, ci sono ancora molte applicazioni circolari se ci guardiamo intorno come pneumatici per auto, monete, orologi da parete, lecca-lecca, nastri DVD, tappi di bottiglia, holahops e altri.

Ok, così importante non è questa forma di cerchio? Ovviamente molto importante. Quindi, impariamo di più sulle formule del cerchio e del cerchio.
Costruisci un cerchio
Un cerchio è una forma bidimensionale costituita da un insieme di punti che formano curve / curve che hanno la stessa lunghezza al centro del cerchio. Qui il punto P è il centro del cerchio.
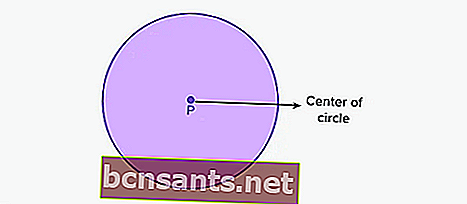
La stessa lunghezza o distanza in tutti i punti dal centro del cerchio è chiamata raggio del cerchio . Nel frattempo, la distanza più lunga che collega i punti esterni di un cerchio è chiamata diametro del cerchio.
Oltre al raggio e al diametro, un cerchio ha altri elementi come un cerchio, un arco circolare, uno scheletro e una corda.
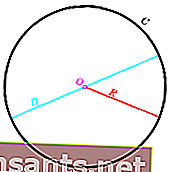
La forma di un cerchio ha anche un'area e una circonferenza. Nella prossima discussione ci concentreremo solo sulla discussione della formula per la circonferenza di un cerchio completo insieme a un problema di esempio.
La formula per la circonferenza di un cerchio
La circonferenza di un cerchio è la distanza da un punto sul cerchio in un giro per tornare al punto originale. oppure può anche essere interpretato come misura della lunghezza del cerchio stesso.
Supponiamo di avere un esperimento, ci sono tre diversi oggetti di forma circolare. Quindi misuriamo la circonferenza e il diametro del cerchio dell'oggetto. Come mostrato nella tabella seguente:
Ad esempio, se abbiamo un braccialetto di metallo. Quindi il braccialetto viene tagliato per formare una barra di metallo dritta, quindi la lunghezza della barra di metallo è la circonferenza del braccialetto o la circonferenza del cerchio.
| Cosa | Circonferenza (K) | Diametro (d) | C / d = π |
| Lattina di soda | 24 cm | 7,7 cm | 3.11 |
| Lattine di latte | 21,5 cm | 7,0 cm | 3.07 |
| Tupperware | 35,5 cm | 11 cm | 3.22 |
Successivamente, calcoliamo il rapporto tra la circonferenza e il diametro e la media dei tre rapporti K / d dell'oggetto è (3,11+ 3,07 +3,22) / 3 = 3,13.
Sì, il rapporto K / d è sempre vicino a 3,14 o 22/7. Ciò significa che il rapporto tra la circonferenza di un cerchio e il diametro è costante o è spesso indicato con π (leggi: phi).
Quindi, il valore di π = C / d = 3,14 o 22/7
Se entrambi i lati vengono moltiplicati per d, otteniamo,
C = π d
Informazione:
K = circonferenza del cerchio
d = diametro del cerchio
π = 3,14 o 22/7
Poiché il diametro è uguale a 2 x il raggio del cerchio d = 2r, la circonferenza del cerchio diventa,
C = πd = π.2r
C = 2 π r
Informazione:
K = circonferenza del cerchio
r = il raggio del cerchio
π = 3,14 o 22/7
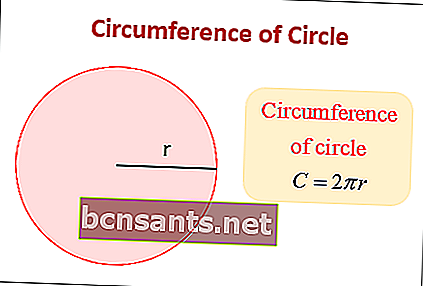
Problema di esempio con la formula della circonferenza
1. La circonferenza di un cerchio è di 396 cm. Calcola il raggio del cerchio!
Noto:
- K = 396 cm
Chiesto:
- r il raggio del cerchio?
Risposta:
C = 2 π r
396 = 2 π r
396,7 = 2. 22/7. r
r = 2772/44
r = 63 cm
Quindi il raggio del cerchio è di 63 cm.
2. Trova la circonferenza di un cerchio con un raggio di 14 cm con π = 22/7
Conosciuto:
- r = 14 cm
- π = 22/7
Chiesto:
- Qual è la circonferenza del cerchio?
Risposta:
C = 2 π r
K = 2 x 22/7 x 14
K = 2 x 22 x 2
K = 88 cm
Quindi, la circonferenza del cerchio è di 88 cm
3. Trova la circonferenza di un cerchio con un diametro di 10 cm con π = 3,14
Conosciuto:
- d = 10 cm
- π = 3,14
Chiesto:
Qual è la circonferenza del cerchio?
Risposta:
C = π d
K = 3,14 x 10
K = 31,4 cm
Quindi la circonferenza del cerchio è di 31,4 cm
4. Calcola la circonferenza dell'area ombreggiata sottostante!
Conosciuto:
- r = 14 cm
Chiesto:
Intorno all'area ombreggiata?
Risposta:
L'immagine sopra la circonferenza è costituita dalla circonferenza di un quadrato più metà del cerchio e sottratta da un semicerchio, con lo stesso diametro e lato del quadrato, quindi la formula per la circonferenza diventa
Leggi anche: I conduttori sono: descrizioni, disegni ed esempiCirconferenza = 14 + 14 + ½ K + ½ K
= 14 + 14 + ½ π d + ½ π d
= 14 + 14 + ½. 22/7. 14 + ½. 22/7. 14
= 28 + 22+ 22
Circonferenza = 72 cm
Quindi la circonferenza dell'area ombreggiata è pari a 72 cm.
5. Budi ha una moto che ha ruote di diametro 84 cm e ruota 1000 volte, calcola quanto ha percorso l'auto?
Conosciuto:
- d = 84 cm
- n = 1000 volte
Chiesto:
Quanto fa la copertura della moto?
Risposta:
La distanza percorsa dal motore per 1000 volte la circonferenza del cerchio = n / 2 = 1000/2 = 500
Quindi la distanza percorsa dal motore = 500x π d = 500.3,14. 84 = 131.880 cm = 1,31 km
6. Qual è la circonferenza del cerchio se il diametro è di 40 cm?
Risposta:
- Perimetro = π xd
- = 3,14 x 40
- = 125,66
Quindi la circonferenza del cerchio è di 125,66 cm.
7. Calcola la circonferenza del cerchio con un diametro di 20 cm?
Soluzione:
Conosciuto:
- d = 20 cm
- π = 3,14
Alla domanda: Intorno al cerchio?
Risposta:
- Circonferenza = π × d
- Circonferenza = 3,14 × 20
- Circonferenza = 62,8 cm
Quindi, la circonferenza del cerchio è di 62,8 cm.
Questa è una spiegazione completa delle formule complete della circonferenza insieme a domande di esempio. Può essere utile!
Riferimento:
- Circonferenze del cerchio - Accademia Khan
- Come calcolare le circonferenze del cerchio - Wikihow
