
La formula della deviazione standard o quella che viene chiamata deviazione standard è una tecnica statistica utilizzata per spiegare l' omogeneità di un gruppo.
La deviazione standard può essere utilizzata anche per spiegare come i dati sono distribuiti in un campione, nonché la relazione tra i singoli punti e il valore medio o medio del campione.
Prima di discutere ulteriormente ci sono alcune cose che dobbiamo sapere prima, vale a dire dove:
La deviazione standard del set di dati può essere zero o maggiore o minore di zero.
Questi valori variabili hanno significati, vale a dire:
- Se la deviazione standard è zero, tutti i valori campione nel set di dati sono uguali.
- Nel frattempo, il valore della deviazione standard maggiore o minore di zero indica che il punto dati dell'individuo è lontano dal valore medio.

Passaggi per trovare la deviazione standard
Per determinare e trovare il valore di deviazione standard dobbiamo seguire i passaggi seguenti.
- Il primo passo
Calcola il valore medio o medio in ogni punto dati.
Puoi farlo sommando ogni valore nel set di dati, quindi il numero viene diviso per il numero totale di punti dai dati.
- Il prossimo passo
Calcola la varianza dei dati calcolando la deviazione o la differenza per ogni punto dati dal valore medio.
Il valore di deviazione in ogni punto dati viene quindi quadrato e rimosso dal quadrato del valore medio.
Dopo aver ottenuto il valore della varianza possiamo calcolare la deviazione standard radicando il valore della varianza.
Leggi anche: Narrazione: definizione, scopo, caratteristiche, tipi ed esempiFormule di deviazione standard
1. Deviazione standard della popolazione
Una popolazione è simbolizzata da σ (sigma) e può essere definita dalla formula:

2. Esempio di deviazione standard
La formula è:
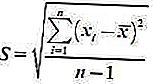
3. La formula per la deviazione standard di molti gruppi di dati
Per scoprire la distribuzione dei dati da un campione, possiamo ridurre ogni valore dei dati del valore medio, quindi vengono aggiunti tutti i risultati.
Tuttavia, se si utilizza il metodo sopra, il risultato sarà sempre zero, quindi quel metodo non può essere utilizzato.

In modo che il risultato non sia zero (0), dobbiamo prima quadrare la riduzione del valore dei dati e del valore medio, quindi sommare tutti i risultati.
Utilizzando questo metodo, il risultato della somma dei quadrati avrà un valore positivo.

Il valore della varianza sarà ottenuto dividendo la somma dei quadrati per il numero di dimensioni dei dati (n).
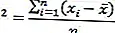
Tuttavia, se utilizziamo questo valore della variante per trovare la varianza della popolazione, il valore della varianza sarà maggiore della variante del campione.
Per ovviare a questo problema, la dimensione dei dati (n) come divisore deve essere sostituita con gradi di libertà (n-1) in modo che il valore della varianza del campione si avvicini alla variante della popolazione.
Pertanto la formula della variante campione può essere scritta come:

Il valore della variante che è stata ottenuta è il valore quadrato, quindi dobbiamo prima quadrarlo per ottenere la deviazione standard.

Per semplificare il calcolo, la formula per la varianza e la deviazione standard può essere ridotta alla formula seguente.
Formule di varianti dei dati
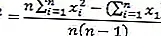
Formula della deviazione standard
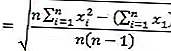
Osservazioni :
s2 = variante
s = deviazione standard
x i = l'i esimo valore x
n = dimensione del campione
Esempio di problemi di deviazione standard
Quello che segue è un esempio e lavora su problemi di deviazione standard.
Domanda:
Sandi, in qualità di presidente dei membri extracurricolari, ha il compito di registrare l'altezza complessiva dei membri. I dati che la password ha raccolto sono i seguenti:
167, 172, 170, 180, 160, 169, 170, 173, 165, 175
Dai dati sopra, calcola la deviazione standard!
Leggi anche: Codice Morse: storia, formule e metodi di memorizzazioneRisposta :
| io | x i | x i 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
Dai dati sopra, si può vedere che il numero di dati (n) = 10 e anche i gradi di libertà (n-1) = 9
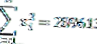
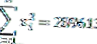
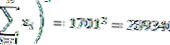
In modo che possiamo calcolare il valore della varianza come segue:

Il valore della variante dei dati raccolti da Sandi è 30,32 . Per calcolare la deviazione standard dobbiamo solo quadrare il valore della varianza in modo che:
s = √30,32 = 5,51
Quindi, la deviazione standard del problema sopra è 5,51
Vantaggi e applicazioni
La deviazione standard è comunemente utilizzata dagli statistici per determinare se i dati rilevati sono rappresentativi dell'intera popolazione.

Ad esempio, qualcuno vuole conoscere il peso di un bambino di 3-4 anni in un villaggio.
Quindi, per renderlo più facile, dobbiamo solo scoprire il peso di pochi bambini e quindi calcolare la media e la deviazione standard.
Dai valori della media e della deviazione standard possiamo rappresentare l'intero peso corporeo dei bambini di 3-4 anni in un villaggio.
Riferimento
- Deviazione standard - Formule su come trovare ed esempi di problemi
- Deviazione standard: formule di calcolo e problemi di esempio
