
L'equazione quadratica è una delle equazioni matematiche della variabile che ha la più alta potenza di due.
La forma generale di un'equazione quadratica o PK è la seguente:
ax 2 + bx + c = 0
dove x è la variabile, a , b è il coefficiente e c è la costante. Il valore di a non è uguale a zero.
Forme del grafico
Se un'equazione quadratica è descritta in termini di coordinate cartesiane (x, y), formerà un grafo parabolico. Pertanto le equazioni quadratiche sono spesso chiamate anche equazioni paraboliche .
Quello che segue è un esempio della forma di questa equazione sotto forma di un grafico parabolico.
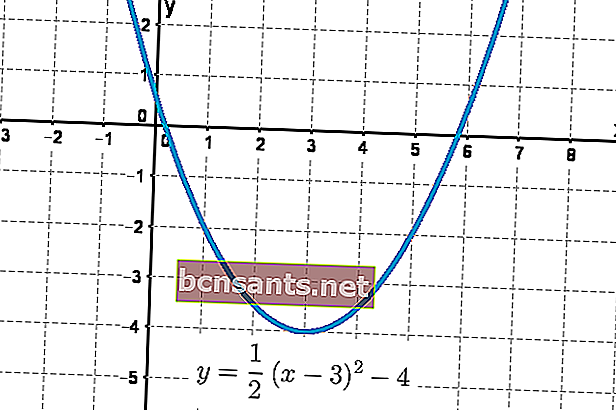
Nell'equazione generale i valori di a , b e c influenzano notevolmente il pattern parabolico risultante.
Il valore di a determina la curva concava o convessa della parabola. Se il valore di a> 0, la parabola si aprirà (concava) . Al contrario, se a <0 , la parabola si aprirà verso il basso (convessa) .

Il valore di b nell'equazione determina il vertice della parabola . In altre parole, determinare il valore dell'asse di simmetria della curva che è uguale ax = - b / 2a .

Il valore costante c sul grafico dell'equazione determina il punto di intersezione della funzione parabola sull'asse y . Quello che segue è un grafico parabolico con variazioni del valore costante c .

Radici dell'equazione quadratica (PK)
La soluzione a un'equazione quadratica è chiamata kar, la radice dell'equazione quadratica .
Varie radici PK
I tipi di radici PK possono essere trovati facilmente usando la formula generale D = b2 - 4ac dall'equazione generale per il quadratico ax2 + bx + c = 0.
I seguenti sono i tipi di radici delle equazioni quadratiche.
1. Radice reale (D> 0)
Se il valore di D> 0 da un PK, produrrà radici di equazioni reali ma con radici diverse. In altre parole x1 non è la stessa cosa di x2.
Esempio dell'equazione della radice reale (D> 0)
Trova il tipo di radice dell'equazione x2 + 4x + 2 = 0.
Soluzione:
a = 1; b = 4; e c = 2
D = b2 - 4ac
D = 42 - 4 (1) (2)
D = 16 - 8
D = 8
Quindi, poiché il valore di D> 0, la radice è di tipo radice reale.
2.La radice reale è uguale a x1 = x2 (D = 0)
È un tipo di radice di un'equazione quadratica che produce radici con lo stesso valore (x1 = x2).
Esempio di radici reali (D = 0)
Trova il valore radice PK di 2x2 + 4x + 2 = 0.
Leggi anche: Tipi di cicli dell'acqua (+ immagine completa e spiegazione)Soluzione:
a = 2; b = 4; c = 2
D = b2 - 4ac
D = 42 - 4 (2) (2)
D = 16-16
D = 0
Quindi, poiché il valore di D = 0, è dimostrato che le radici sono reali e gemellate.
3. Radici immaginarie / Non reali (D <0)
Se il valore di D <0, la radice dell'equazione quadratica sarà immaginaria / non reale.
Esempio di radici immaginarie (D <0) /
Trova il tipo di radice dell'equazione x2 + 2x + 4 = 0.
Soluzione:
a = 1; b = 2; c = 4
D = b2 - 4ac
D = 22 - 4 (1) (4)
D = 4-16
D = -12
Quindi, poiché il valore di D <0, la radice dell'equazione è una radice irreale o immaginaria.
Trova le radici dell'equazione quadratica
Esistono diversi metodi che possono essere utilizzati per trovare le radici di un'equazione quadratica. Tra questi ci sono la fattorizzazione, i quadrati perfetti e l'uso della formula abc.
Di seguito vengono descritti diversi metodi per trovare le radici delle equazioni.
1. Fattorizzazione
La fattorizzazione / factoring è un metodo per trovare le radici cercando un valore che, se moltiplicato, produrrà un altro valore.
Esistono tre forme di equazioni quadratiche (PK) con diversa fattorizzazione delle radici, vale a dire:
| No. | Modulo di equazione | Fattorizzazione radice-radice |
| 1 | x 2 + 2xy + y 2 = 0 | (x + y) 2 = 0 |
| 2 | x 2 - 2xy + y 2 = 0 | (x - y) 2 = 0 |
| 3 | x 2 - y 2 = 0 | (x + y) (x - y) = 0 |
Quello che segue è un esempio di un problema sull'utilizzo del metodo di fattorizzazione nelle equazioni quadratiche.
Risolvi l'equazione quadratica 5x 2 + 13x + 6 = 0 usando il metodo di fattorizzazione.
Soluzione:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x (x + 2) + 3 (x + 2) = 0
(5x + 3) (x + 2) = 0
5x = -3 oppure x = -2
Quindi, la soluzione sarà x = -3/5 o x = -2
2. Quadrati perfetti
La forma quadratica perfetta è un'equazione quadratica che produce numeri razionali .
I risultati di un'equazione quadratica perfetta utilizzano generalmente la seguente formula:
(x + p) 2 = x2 + 2px + p2
La soluzione generale per l'equazione quadratica perfetta è la seguente:
(x + p) 2 = x2 + 2px + p2
con (x + p) 2 = q, quindi:
(x + p) 2 = q
x + p = ± q
x = -p ± q
Quello che segue è un esempio di un problema sull'utilizzo del metodo dell'equazione perfetta.
Risolvi l'equazione x2 + 6x + 5 = 0 usando il metodo dell'equazione quadratica perfetta!
Soluzione:
x2 + 6x +5 = 0
x2 + 6x = -5
Il passaggio successivo consiste nell'aggiungere un numero sui lati destro e sinistro in modo che possa trasformarsi in un quadrato perfetto.
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x + 3) 2 = 4
(x + 3) = √4
x = 3 ± 2
Quindi, il risultato finale è x = -1 o x = -5
Leggi anche: Definizione e differenza di omonimi, omofoni e omografi3. Formule quadratiche ABC
La formula abc è una scelta alternativa quando l'equazione quadratica non può essere risolta con la fattorizzazione o con metodi quadratici perfetti.
La seguente è la formula abc per l'equazione quadratica ax2 + bx + c = 0.
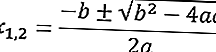
Di seguito è riportato un esempio di risoluzione di un problema di equazione quadratica utilizzando la formula abc .
Risolvi l'equazione x2 + 4x - 12 = 0 usando il metodo della formula abc!
Soluzione:
x2 + 4x - 12 = 0
dove a = 1, b = 4, c = -12

Costruire una nuova equazione quadratica
Se in precedenza abbiamo imparato come trovare le radici dell'equazione, ora impareremo a comporre l'equazione quadratica dalle radici che sono state precedentemente note.
Ecco alcuni modi in cui puoi creare un nuovo PK.
1. Costruisci equazioni quando le radici sono note
Se un'equazione ha radici x1 e x2, l'equazione per quelle radici può essere espressa in termini di
(x- x 1 ) (x- x 2 ) = 0
Esempio:
Trova un'equazione quadratica in cui le radici sono comprese tra -2 e 3.
Soluzione:
x 1 = -2 ex 2 = 3
(x - (- 2)) (x-3) = 0
(x + 2) (x + 3)
x2-3x + 2x-6 = 0
x2-x-6 = 0
Quindi, il risultato dell'equazione per queste radici è x2-x-6 = 0
2. Costruisci un'equazione quadratica se conosci il numero e il prodotto delle radici
Se le radici dell'equazione quadratica con il numero e le volte x1 e x2 sono note, l'equazione quadratica può essere convertita nella forma seguente.
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
Esempio:
Trova un'equazione quadratica con radici 3 e 1/2.
Soluzione:
x 1 = 3 e x 2 = -1/2
x 1+ x 2 = 3-1/2 = 6/2 - 1/2 = 5/2
x 1. x 2 = 3 (-1/2) = -3/2
Pertanto, l'equazione quadratica è:
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
x2– 5/2 x - 3/2 = 0 (ogni lato moltiplicato per 2)
2x2-5x-3 = 0
Quindi, l'equazione quadratica per le radici 3 e 1/2 è 2x2-5x-3 = 0.
