
La frequenza prevista èil numero di apparizioni attese in un evento conducendo ripetutamente esperimenti noti anche come test sperimentali.
Oppure il prodotto della probabilità di accadimento, ad esempio, l'evento A con il numero di esperimenti eseguiti.
In poche parole, hai mai interpretato Ludo? Lancia due dadi contemporaneamente e ti aspetti che un sei appaia su entrambi i dadi? Se è così, significa che hai applicato la teoria della frequenza attesa .
Formule di frequenza previste
In generale, la formula per la frequenza prevista è la seguente:
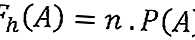
Informazione:
F h (A) = la frequenza attesa di un evento A
n = numero di occorrenze A
P (A) = probabilità di un evento A.
Esempi di domande sulla frequenza prevista
Problema di esempio 1
- I due dadi vengono lanciati insieme 144 volte. Determina la possibilità che sorga la speranza
- I sei su entrambi muoiono.
- Il numero ammonta a sei su entrambi i dadi.
Soluzione:
Per risolvere un problema come questo, calcola prima il numero totale di occorrenze. Tutti gli eventi sono indicati con S, quindi:
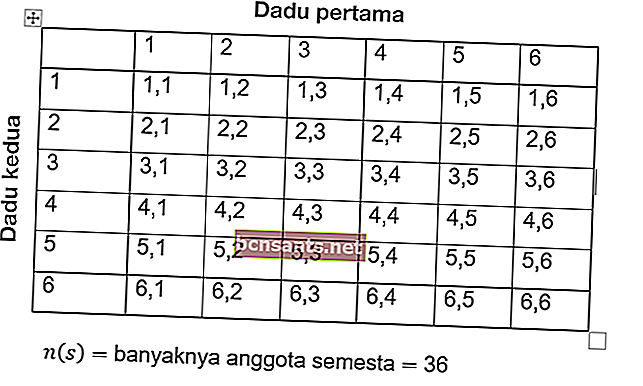
In modo che il numero di membri dell'universo dei numeri sia n (s) = 36.
1. La comparsa del numero sei su entrambi i dadi.
Per i due numeri che compaiono solo uno, ovvero (6,6), allora:
n (1) = 1
Allora il numero di esperimenti era 144 volte
n = 144
Quindi,
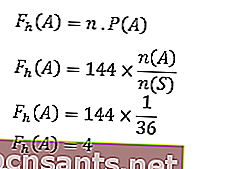
Quindi, la frequenza prevista per la comparsa del numero sei su entrambi i dadi è 4 volte.
2. La comparsa del numero di dadi che totalizza sei
Per il numero di dadi che totalizzano sei, vale a dire

Allora il numero di esperimenti era 144 volte

Quindi,

Quindi, la frequenza prevista per la comparsa di sei dadi è 20 volte.
Esempio problema 2
Una moneta che è stata lanciata in aria 30 volte. Determina la frequenza di apparizione prevista sul lato numerico.
Leggi anche: Formule di accelerazione + Esempi di problemi e soluzioniSoluzione:
L'universo di questo incidente è solo due, vale a dire il lato del numero e il lato dell'immagine, o scritto

quindi, n (S) = 2
Il numero di monete lanciate è 30 volte, quindi n = 30
C'è solo un lato di un numero, quindi n (A) = 1
La frequenza prevista degli eventi è,
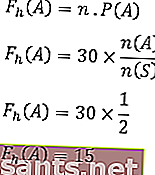
Pertanto, la frequenza prevista di comparsa del lato numerico è 20 volte.
Conclusione
Quindi la frequenza attesa è una frequenza o il numero di prove moltiplicato per la probabilità di un evento risultante nel numero di aspettative che compaiono su un particolare evento.
Quindi, dopo la spiegazione sopra, puoi calcolare le tue speranze di vincere una lotteria? Quali trucchi dovresti fare per aumentare le tue speranze di vittoria?
Scrivi il tuo trucco infallibile nei commenti e faglielo sapere.
Quindi una spiegazione della formula e della comprensione, nonché esempi della frequenza delle aspettative, si spera che sia utile e ci vediamo nel prossimo materiale
