
Se parli di formule, figuriamoci di fisica, sarai sempre contattato per memorizzare domande. Fondamentalmente, la formula non deve essere memorizzata ma deve solo essere compresa. Ora ti aiuterò a non memorizzare una formula. Nemmeno i suggerimenti relativi all'elaborazione del cervello per memorizzarlo, niente affatto, amici miei. Quindi lascia che ti presenti, Dimensions of Magnitude!
Quindi, se sei un figlio della fisica, sicuramente avrai familiarità con il nome Dimensione della quantità. Quindi saprai che ci sono 7 quantità principali e le loro unità. Quindi queste sette quantità hanno anche le loro dimensioni. Quindi puoi vedere di più qui sotto.

E per alcune quantità derivate, le dimensioni saranno così
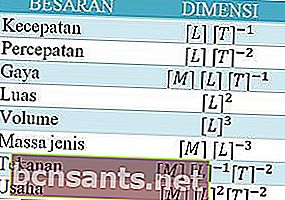
Quindi cosa ha a che fare con il non conoscere la formula?

Quindi ti farò un esempio. Supponi di aver dimenticato la formula per il periodo di un pendolo. Quello che ti ricordi è che ha un valore costante di 2 pi ed è correlato alla lunghezza della fune e all'accelerazione dovuta alla gravità e quindi pensi che la massa del pendolo abbia un effetto. Va bene quindi iniziamo.
Prima di tutto elencherai prima quali grandezze influenzano il periodo del pendolo e come sopra menzionato,
- Lunghezza corda (l)
- Accelerazione dovuta alla gravità (g)
- Massa del pendolo (m)
Bene e ora facciamo la magia. Per il periodo stesso la quantità è il tempo, la lunghezza della fune è la lunghezza e l'accelerazione dovuta alla gravità che è una grandezza derivata che dipende dalla lunghezza e dal tempo. Va bene per il prossimo possiamo farlo in questo modo:
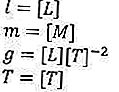
Ad ogni modo, anche qui è molto necessaria la conoscenza di base degli esponenti, quindi è meglio prima di continuare, assicurati di aver padroneggiato gli esponenti e non dimenticare l'algebra ovviamente.
Leggi anche: La formula per il perimetro di un triangolo (spiegazione, domande di esempio e discussione)Ora quindi creiamo l'equazione in questo modo
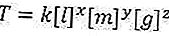
Allora perché ci sono variabili? Sì, perché ancora non sappiamo che la formula sarà così, ecco perché diamo una variabile lì. Allora perché non per T (punto)? Perché sappiamo certamente che in quel periodo l'unità è solo pochi secondi per un grado, e che ne dici. E per k stesso, è una costante che non influenzerà la soluzione in seguito. Ok, puoi capire, quindi cerchiamo il valore di ciascuna variabile
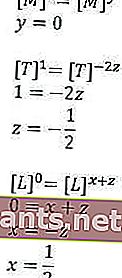
In questo modo possiamo ottenere la formula sostituendo i valori che sono stati ottenuti
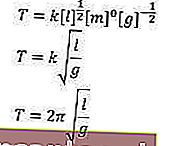
Sì, abbiamo capito, fratello.

Bene, questo è ciò che viene spesso chiamato analisi dimensionale. L'analisi dimensionale è molto utile per scienziati e ingegneri esistenti per effettuare calcoli precisi. Quindi rimanete ragazzi!
Questo post è il contributo dell'autore. Puoi anche creare i tuoi scritti su Saintif unendoti alla Comunità Saintif
Riferimento:
Giancoli, Douglas. 2014. Principi di fisica con applicazioni 7a ed. New Jersey: PEARSON Prentice Hall
