
L'integrale indefinito o anche noto come anti-derivato è una forma di operazione di integrazione che produce una nuova funzione .
L'integrale gioca un ruolo molto importante in matematica. La teoria può determinare l'area sotto la curva di una funzione.
Integrale è utile per il limite di somma che è continuo su una funzione continua. L'integrale è anti-derivato. Quindi, se f è una funzione continua, il risultato integrale della funzione f è indicato con F.
I tipi integrali basati su determinati confini funzionali non sono certi. Quanto segue è una discussione per i tipi di integrali con limiti indefiniti.
Integrale indefinito
Un integrale indefinito o noto anche come anti-derivativo o anti-diverenziale è una forma di operazione di integrazione che produce una nuova funzione.
Considera la seguente equazione.

con C una costante. La formula integrale indefinita è la seguente
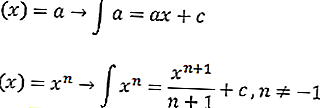
o uguale a

con
- a (x) ^ n = funzione di equazione
- a = Costante
- x = variabile
- n = Potenza della funzione dell'equazione
- C = costante
Il risultato di questo integrale indefinito è una funzione che è una nuova funzione che non ha un valore certo o definito perché ci sono ancora variabili nella nuova funzione.
Per comprendere meglio il concetto di integrali indeterminati, considera le domande di esempio di seguito.

Sulla base di questo esempio, è possibile formulare un'operazione integrale, vale a dire
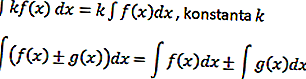
Integrale trigonometrico
L'integrale di una funzione indefinita non è solo una costante, lineare o polinomiale. In questa soluzione intergal, spesso coinvolge elementi trigonometrici.
Nella funzione trigonomica vale anche la definizione di integrali che è disposta nella tabella seguente.
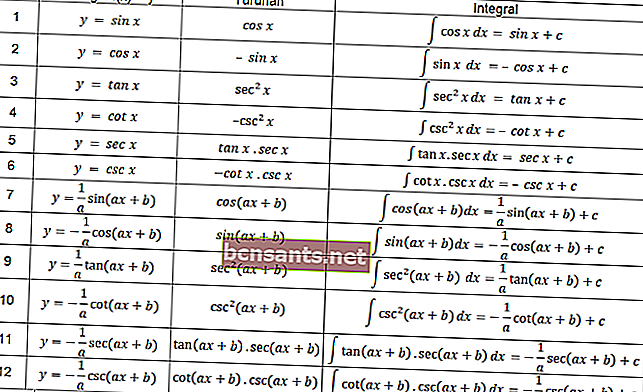
È possibile utilizzare le equazioni nella tabella sopra per risolvere il problema integrale che coinvolge la trigonometria.
Per comprendere meglio gli integrali trigonometrici puoi comprendere i seguenti esempi
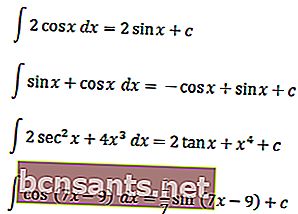
Questa era la spiegazione degli integrali indeterminati nelle funzioni trigonometriche ordinarie e speciali. Si spera che possa essere studiato bene.
Leggi anche: Le norme della decenza: definizione, scopo, sanzioni ed esempi [COMPLETO]Per comprendere meglio il concetto di questo integrale, puoi esercitarti a fare domande pratiche. Se c'è qualcosa che vuoi chiedere, annotalo nella colonna dei commenti.
