
Il valore assoluto nel calcolo è molto utile per risolvere vari problemi matematici, sia nelle equazioni che nelle disequazioni. Quanto segue è una spiegazione completa dei valori assoluti e delle domande campione.
Definizione di valore assoluto
Tutti i numeri hanno i rispettivi valori assoluti. Tutti i numeri assoluti sono positivi, quindi i valori numerici assoluti di numeri con lo stesso numero ma la differenza tra notazioni positive (+) e negative (-) avranno lo stesso risultato numerico assoluto.
Se x è un membro di un numero reale, il valore assoluto viene scritto come | x | ed è definito come segue:

"Il valore assoluto è un numero con lo stesso valore di lunghezza o distanza dall'origine o punto zero nelle coordinate."
Si può interpretare che il valore assoluto di 5 è la lunghezza o la distanza dal punto 0 al punto 5 o (-5).
I valori assoluti di (-9) e 9 sono 9. Il valore assoluto di 0 è 0 e così via. Nilaa
Lo capirò assolutamente guardando la seguente immagine:

Nell'immagine sopra, si può capire che il valore di | 5 | è la distanza del punto 5 dal numero 0, ovvero 5, e | -5 | la distanza del punto (-5) dal numero 0 è 5.
Se | x | rappresenta la distanza dal punto x a 0, quindi | xa | è la distanza dal punto x al punto a. Ad esempio, quando si esprime la distanza dal punto 5 al punto 2, potrebbe essere scritto come | 5-2 | = 3

In generale, si può affermare che la distanza da x ad a può essere scritta con la notazione | xa | o | ax |
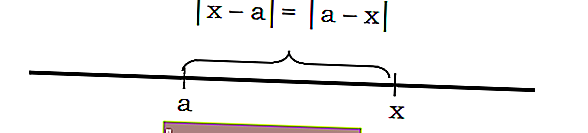
Ad esempio, la distanza di un numero dal punto 3 vale 7 come segue:
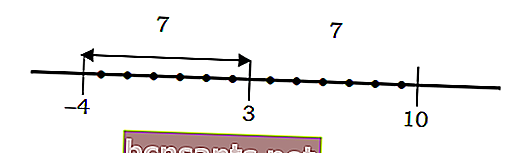
Se descritto nell'equazione algebrica | x-3 | = 7 può essere risolto come segue:
Leggi anche: Misurare i terremoti con i logaritmi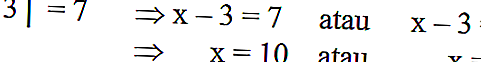
Ricorda che | x-3 | è la distanza del numero x dal punto 3, dove | x-3 | = 7 è la distanza del numero x dal punto 3 per 7 unità.
Proprietà di valore assoluto
Nelle operazioni di equazioni di numeri assoluti, esistono proprietà di numeri assoluti che possono aiutare a risolvere equazioni di numeri assoluti.
Di seguito sono riportate le proprietà dei numeri assoluti in generale nelle equazioni del valore assoluto:

Le proprietà del valore assoluto della disuguaglianza:
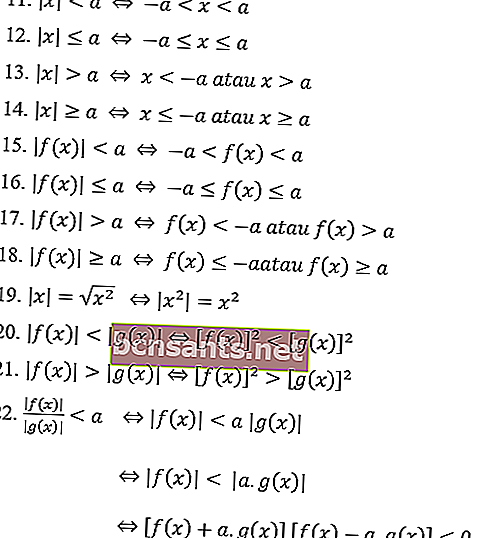
Esempi di problemi con l'equazione del valore assoluto
Problema di esempio 1
Qual è il valore assoluto dell'equazione | 10-3 |?
Risposta:
| 10-3 | = | 7 | = 7
Problema di esempio 2
Qual è il risultato di x per l'equazione per il valore assoluto | x-6 | = 10?
Risposta:
Per risolvere questa equazione, ci sono due possibili risultati per i numeri assoluti
| x-6 | = 10
Prima soluzione:
x-6 = 10
x = 16
seconda soluzione:
x - 6 = -10
x = -4
Quindi, la risposta a questa equazione è 16 o (-4)
Problema di esempio 3
Risolvi e calcola il valore x nella seguente equazione
–3 | x - 7 | + 2 = –13
Risposta:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
Fatto fino alla soluzione sopra, il valore x ha due valori
x - 7 = 5
x = 12
o
x - 7 = - 5
x = 2
quindi il valore x finale è 12 o 2
Problema di esempio 4
Risolvi la seguente equazione e qual è il valore x
| 7 - 2x | - 11 = 14
Risposta:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
Dopo aver completato l'equazione precedente, i numeri per il valore assoluto di x sono i seguenti
7 - 2x = 25
2x = - 18
x = - 9
o
7 - 2x = - 25
2x = 32
x = 16
Quindi il valore x finale è (- 9) o 16
Problema di esempio 5
Trova la soluzione alla seguente equazione del valore assoluto:
| 4x - 2 | = | x + 7 |
Risposta:
Per risolvere l'equazione di cui sopra, utilizzare due possibili soluzioni, vale a dire:
Leggi anche: Errori nella lettura dei risultati statistici del sondaggio sull'elezione dei candidati alla presidenza4x - 2 = x + 7
x = 3
o
4x - 2 = - (x + 7)
x = - 1
Quindi la soluzione per l'equazione | 4x - 2 | = | x + 7 | è x = 3 oppure x = - 1
Problema di esempio 6
Determina la soluzione alla seguente equazione del valore assoluto:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
Qual è il valore di x?
Risposta:
Semplificazione: | 3x + 2 | = p
poi
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (il valore assoluto non è negativo)
o
p - 1 = 0
p = 1
| 3x + 2 | = 1
Fino alla soluzione sopra, ci sono 2 possibili risposte per x, vale a dire:
3x + 2 = 1
3x = 1 - 2
3x = - 1
x = - 1/3
o
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1 - 2
3x = - 3
x = - 1
Quindi la soluzione dell'equazione è x = - 1/3 ox = - 1
Riferimento: valore assoluto - La matematica è divertente
