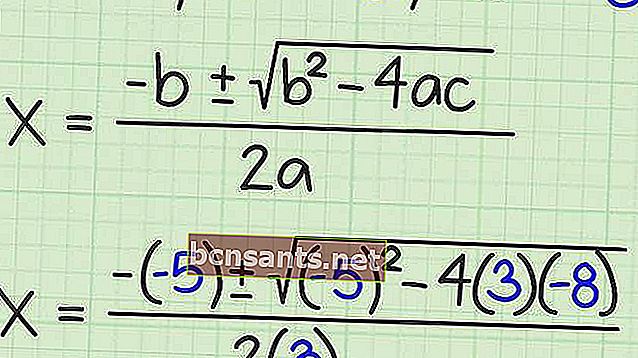
La formula ABC è un ottimo modo per trovare le radici di varie forme di equazioni quadratiche anche se il risultato non è un numero intero.
L'equazione quadratica ax2 + bx + c = 0 può essere risolta utilizzando diversi metodi. Tra questi ci sono il metodo di factoring, completando il quadrato ABC e la formula.
Tra questi metodi, la formula abc è eccellente perché può essere utilizzata per trovare le radici di varie forme di equazioni quadratiche anche se il risultato non è un numero intero.
Quanto segue è un'ulteriore spiegazione della formula, inclusa la comprensione, le domande e la discussione.
Capire la formula ABC
La formula abc è una delle formule utilizzate per trovare le radici di un'equazione quadratica. Ecco una forma generale di questa formula.

Le lettere a, b e c nella formula abc sono chiamate coefficienti. Il coefficiente di x2 al quadrato è a, il coefficiente di x è be c è il coefficiente di costante, di solito indicato come termine costante o indipendente.
L'equazione quadratica è fondamentalmente un'equazione matematica che forma la geometria curva della parabola nel quadrante xy.
Il valore del coefficiente nella formula abc ha diversi significati come segue:
- a determina la prabola concava / convessa formata dall'equazione quadratica. Se il valore di a> 0 la parabola si aprirà verso l'alto. Tuttavia, se a <0, la parabola si aprirà verso il basso.
- b determina la posizione x del picco del parabol, o la simmetria speculare della curva. La posizione esatta dell'asse di simmetria è -b / 2a dell'equazione quadratica.
- c determina l'intersezione della funzione di equazione quadratica parabolica formata sull'asse y quando il valore x = 0.
Domande di esempio e discussione
Di seguito sono riportati alcuni esempi di problemi di equazioni quadratiche e la loro discussione con soluzioni utilizzando formule di equazioni quadratiche.
1. Risolvi le radici dell'equazione quadratica x2 + 7x + 10 = 0 usando la formula abc!
Risposta:
Leggi anche: 7 funzioni proteiche per il corpo [spiegazione completa]nota che a = 1, b = 7 e c = 10
quindi, le radici dell'equazione sono:

Quindi, il prodotto delle radici dell'equazione x2 + 7x + 10 = 0 è x = -2 o x = -5
2. Utilizzando la formula abc, trova l'insieme di soluzioni per x2 + 2x = 0
Risposta:
dato che a = 1, b = 1, c = 0
quindi le radici dell'equazione sono le seguenti:

Quindi, il prodotto delle radici dell'equazione x2 + 2x = 0 è x1 = 0 e x2 = -2, quindi l'insieme di soluzioni è HP = {-2,0}
3. Trova l'insieme di radici x nel problema x2 - 2x - 3 = 0 usando la formula abc
Risposta:
dato che a = 1, b = 2, c = -3
quindi i risultati delle radici dell'equazione sono i seguenti:

Quindi, con x1 = -1 e x2 = -3, l'insieme di soluzioni è HP = {-1,3}
4. Determina il risultato dell'equazione quadratica x 2 + 12x + 32 = 0 usando la formula abc !
Risposta:
nota che a = 1, b = 12 e c = 32
quindi le radici dell'equazione sono le seguenti:

Quindi, i risultati delle radici per l'equazione quadratica sono -4 e -8
5. Trova l'insieme dal seguente problema 3x2 - x - 2 = 0
Risposta:
nota che a = 3, b = -1, c = -2
quindi le radici dell'equazione sono le seguenti:

Pertanto, le radici dell'equazione quadratica 3x2 - x - 2 = 0 sono x1 = 1 e x2 = -2 / 3, quindi l'insieme di soluzioni è HP = {1, -2 / 3}
6. Trova le radici dell'equazione x 2 + 8x + 12 = 0 usando la formula abc!
Risposta:
nota che a = 1, b = 8 e c = 12
quindi le radici dell'equazione quadratica sono le seguenti:

Pertanto, le radici dell'equazione quadratica x2 + 8x + 12 = 0 sono x1 = -6 o x2 = -2 in modo che l'insieme di soluzioni sia HP = {-6, -2}
7. Risolvi le radici dell'equazione x 2 - 6x - 7 = 0 con la formula abc .
Risposta:
è noto che a = 1, b = - 6 e c = - 7
quindi le radici dell'equazione sono le seguenti:
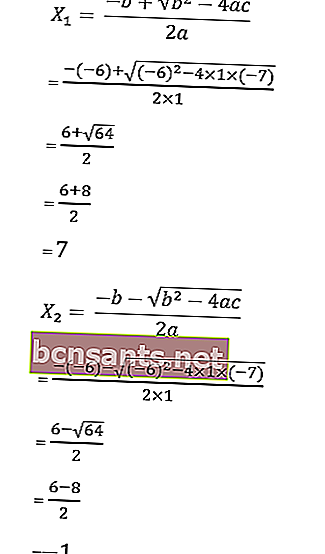
Quindi le radici sono x 1 = 1 o x 2 = 5/2, quindi l'insieme di soluzioni è HP = {1, 5/2}.
Leggi anche: Equazioni quadratiche (COMPLETE): definizione, formule, problemi di esempio8. Trova le radici dell'equazione 2x 2 - 7x + 5 = 0 con la formula abc
Risposta:
dato che a = 2, b = - 7 e c = 5
quindi le radici dell'equazione sono le seguenti:
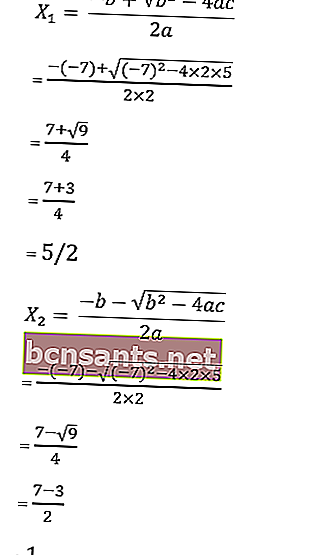
Quindi le radici sono x1 = –4 o x2 = 5/3 in modo che l'insieme di soluzioni sia HP = {1, 5/3}.
9. Risolvi l'equazione 3x 2 + 7x - 20 = 0 con la formula abc.
Risposta:
nota che a = 3, b = 7 e c = - 20
quindi le radici dell'equazione sono:
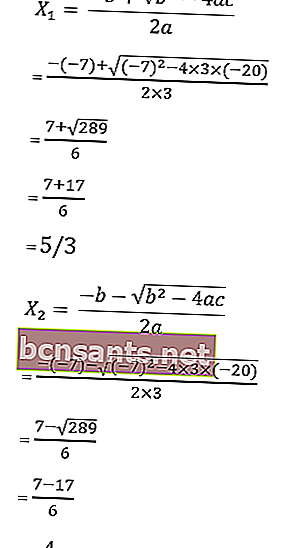
Quindi le radici sono x1 = –4 o x2 = 5/3, quindi l'insieme di soluzioni è HP = {-4, 5/3}.
10. Trova le radici dell'equazione 2x 2 + 3x +5 = 0 con la formula abc.
Risposta:
noto che a = 2, b = 3 e c = 5
quindi le radici dell'equazione sono le seguenti:
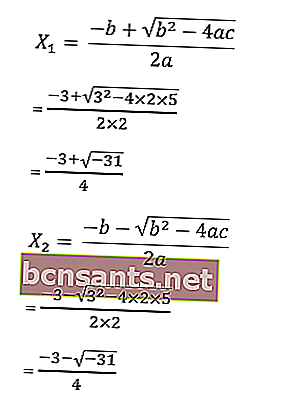
Il risultato della radice dell'equazione 2x2 + 3x +5 = 0 ha il numero della radice immaginaria √ - 31, quindi l'equazione non ha soluzione. L'insieme di soluzioni è scritto come l'insieme vuoto HP = {∅}
Questa è una spiegazione della definizione della formula abc con esempi di domande e la loro discussione. Può essere utile!
