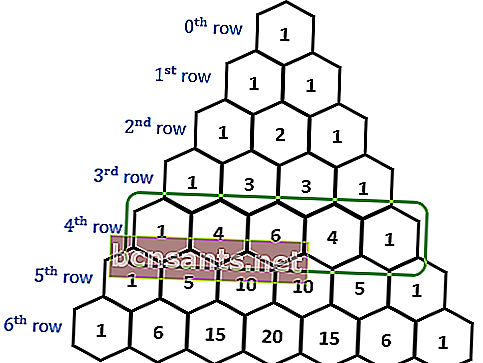
Il triangolo di Pascal è una disposizione di triangoli creata sommando elementi adiacenti nella riga precedente. Questa disposizione dei triangoli si ottiene aggiungendo elementi adiacenti nella riga precedente.
Supponiamo che le variabili aeb siano sommate insieme, quindi elevate alla potenza da 0 a 3, il risultato è la seguente descrizione.
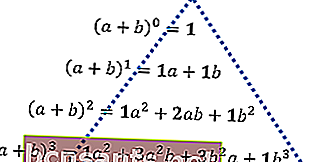
Quindi, considera la disposizione dei numeri in grassetto dall'alto verso il basso, fino a trovare una forma triangolare. Questo modello numerico è di seguito denominato triangolo Pascal.
Capire il triangolo di Pascal
Il triangolo di Pascal è la regola geometrica sul coefficiente binomiale di un triangolo.
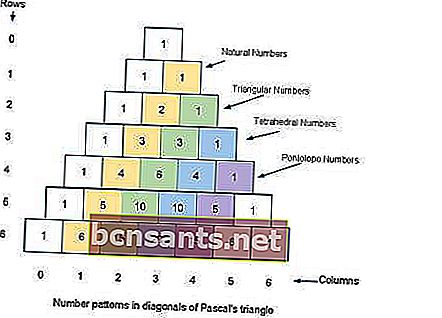
Il triangolo prende il nome dal matematico Blaise Pascal, sebbene altri matematici lo abbiano studiato secoli prima di lui in India, Persia, Cina e Italia.
Concetto di regole
Il concetto di triangolo Pascal è un sistema di calcolo per questo triangolo indipendentemente dalle variabili a e b. Ciò significa che è sufficiente prestare attenzione al coefficiente binomiale, come segue:
- Nella riga zero, scrivi solo il numero 1.
- In ogni riga sottostante, scrivi il numero 1 a sinistra ea destra.
- La somma dei due numeri sopra, poi scritti sulla riga sotto.
- Il numero 1 a sinistra ea destra secondo (2), circonda sempre il risultato (3)
- I calcoli possono essere continuati con lo stesso schema.
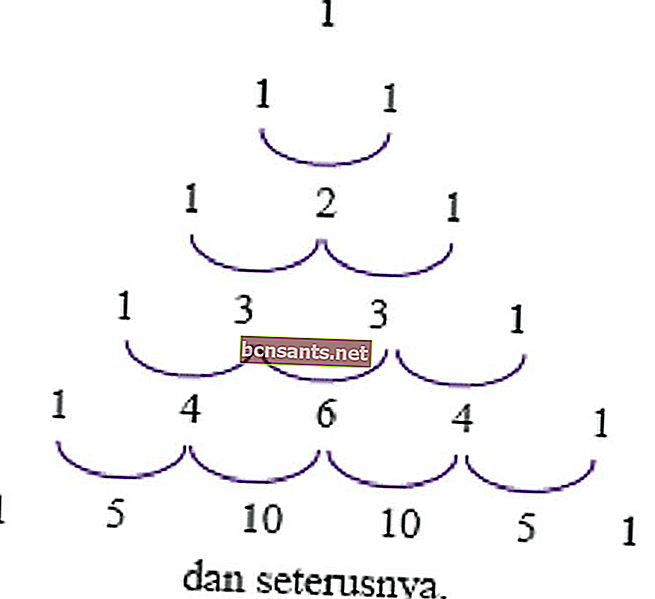

Un uso di questo triangolo è determinare il coefficiente di potenza (a + b) o (ab) per renderlo più efficiente. Questo utilizzo è descritto nei seguenti esempi.
Esempio di problemi
Suggerimento: presta attenzione al triangolo di Pascal.
1. Qual è la traduzione (a + b) 4?
Soluzione : per (a + b) 4
- Per prima cosa vengono disposte le variabili aeb, a partire da a4b o a4
- Quindi la potenza di a scende a 3, che è a3b1 (la potenza totale di ab deve essere 4)
- Quindi la potenza di a scende a 2, diventando a2b2
- Quindi la potenza di a scende a 1, diventando ab3
- Quindi la potenza di a scende a 0, a b4
- Quindi scrivi l'equazione con il coefficiente davanti allo spazio vuoto
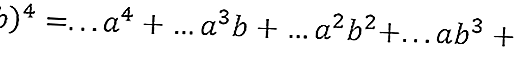
Secondo la Figura 2 nel 4 ° ordine si ottengono i numeri 1,4,6,4,1, quindi si ottiene la traduzione (a + b) 4

2. Qual è il coefficiente a3b3 in (a + b) 6?
Leggi anche: Materiale del campo magnetico: formule, esempi di problemi e spiegazioniSoluzione :
In base alla domanda numero 1, l'ordine delle variabili da (a + b) 6 è organizzato, ovvero
a6, a5b1, a4b2, a 3 b 3 .
Ciò significa che al quarto posto (immagine 2, sequenza 6) nello schema 1, 6, 15, 20 c'è 20 . Pertanto, è possibile scrivere 20 a3b3.
3. Determina la traduzione di (3a + 2b) 3
Insediamento
La formula generale per il triangolo pascal come somma delle variabili aeb alla potenza di 3 è presentata come segue

Modificando le variabili in 3a e 2b, otteniamo

